well the limit of 0,999.. is 1 when digits goes to infinity so the outcome is right. my mistake.
but you type it with a misleading way . not proper.
Which one? | |||
| Maths | 19 | 26.76% | |
| Math | 20 | 28.17% | |
| Mathematics | 32 | 45.07% | |
| Total: | 71 | ||
well the limit of 0,999.. is 1 when digits goes to infinity so the outcome is right. my mistake.
but you type it with a misleading way . not proper.
Teeqoz said:
Yes I can, because I've defined x = 0.999... |
No you can't. Your replacement changes the whole equation. That's not how algebra works. I cannot randomly replace numbers out of the blue. And say x is still what it was in the previous equation. You cannot say 0.9999 is 1 when you changed x to 1.
Intel Core i7 8700K | 32 GB DDR 4 PC 3200 | ROG STRIX Z370-F Gaming | RTX 3090 FE| Crappy Monitor| HTC Vive Pro :3
OP is correct! There will be no arguing that fact ...
We can use an infinite series (assumed seceond semester calculus) to prove such or a simple algebraic proof in the OPs case ...
Here's the infinite series ... 
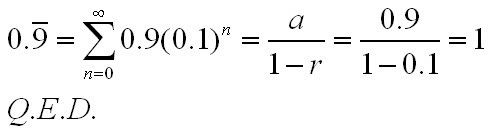
| Platina said: Math doesn't work that way though it does look neat [1/9]*9 = 1, not 0.999... |
Yes, it does work that way ^^.
1/3 = 0.333333333333...
3*(1/3) = 3*0.3333333333....
3*(1/3) = 1
3*0.3333333333333.... = 0.999999999999...
So 0.9999999999... = 1
It's pretty funny to read debates here (even if there should be any debate on that proven fact) and to read the following :
|
Students of mathematics often reject the equality of 0.999… and 1, for reasons ranging from their disparate appearance to deep misgivings over the limit concept and disagreements over the nature of infinitesimals. There are many common contributing factors to the confusion:
These ideas are mistaken in the context of the standard real numbers, although some may be valid in other number systems, either invented for their general mathematical utility or as instructive counterexamples to better understand 0.999… Many of these explanations were found by David Tall, who has studied characteristics of teaching and cognition that lead to some of the misunderstandings he has encountered in his college students. Interviewing his students to determine why the vast majority initially rejected the equality, he found that "students continued to conceive of 0.999… as a sequence of numbers getting closer and closer to 1 and not a fixed value, because 'you haven't specified how many places there are' or 'it is the nearest possible decimal below 1'".[38] Of the elementary proofs, multiplying 0.333… = 1⁄3 by 3 is apparently a successful strategy for convincing reluctant students that 0.999… = 1. Still, when confronted with the conflict between their belief of the first equation and their disbelief of the second, some students either begin to disbelieve the first equation or simply become frustrated.[39] Nor are more sophisticated methods foolproof: students who are fully capable of applying rigorous definitions may still fall back on intuitive images when they are surprised by a result in advanced mathematics, including 0.999…. For example, one real analysis student was able to prove that 0.333… = 1⁄3 using a supremum definition, but then insisted that 0.999… < 1 based on her earlier understanding of long division.[40] Others still are able to prove that 1⁄3 = 0.333…, but, upon being confronted by the fractional proof, insist that "logic" supersedes the mathematical calculations. Joseph Mazur tells the tale of an otherwise brilliant calculus student of his who "challenged almost everything I said in class but never questioned his calculator," and who had come to believe that nine digits are all one needs to do mathematics, including calculating the square root of 23. The student remained uncomfortable with a limiting argument that 9.99… = 10, calling it a "wildly imagined infinite growing process."[41] As part of Ed Dubinsky's APOS theory of mathematical learning, he and his collaborators (2005) propose that students who conceive of 0.999… as a finite, indeterminate string with an infinitely small distance from 1 have "not yet constructed a complete process conception of the infinite decimal". Other students who have a complete process conception of 0.999… may not yet be able to "encapsulate" that process into an "object conception", like the object conception they have of 1, and so they view the process 0.999… and the object 1 as incompatible. Dubinsky et al. also link this mental ability of encapsulation to viewing 1⁄3 as a number in its own right and to dealing with the set of natural numbers as a whole.[42] |
Its even funnier to read these (I love the last one :D )
|
The lower primate in us still resists, saying: .999~ doesn't really represent a number, then, but a process. To find a number we have to halt the process, at which point the .999~ = 1 thing falls apart. Nonsense.[44] |
|
Q: How many mathematicians does it take to screw in a lightbulb? A: 0.999999…. |
EDIT : Well, the formatting seems to crop a part, but it's on the Wiki anyway!
| fatslob-:O said: OP is correct! There will be no arguing that fact ... We can use an infinite series (assumed seceond semester calculus) to prove such or a simple algebraic proof in the OPs case ... Here's the inifinite series ...
|
Well the limit -> infinity is 1 not just x. it was misleading.
because 0,9999 isn't equal to 1.
| Platina said: Math doesn't work that way though it does look neat [1/9]*9 = 1, not 0.999... |
Actually math does work that way.
And 1/9*9=1=0.999... 
1/9=0.111... you agree on this, right?
and 0.111...*9=0.999... you agree on this as well, right?
Now, since 0.111... = 1/9, and 0.111....*9=0.999... then 0.999....=1
Peh said:
No you can't. Your replacement changes the whole equation. That's not how algebra works. I cannot randomly replace numbers out of the blue. Faelco explained it pretty well here, so I'll just give you his reply to someone questioning the same thing. |
Faelco said:
The "If x=0.999999..." or equivalent is basically the first sentence of any mathematical problem or demonstration. Of course you can replace your "0.999999999..." by x. |

Faelco said:
0.999999 = 1 is wrong. 0.9999999.... = 1 is true. That 0.0000001 part doesn't exist with an infinity of 9.
It is basic mathematics, you can learn it in school (okay, it's more often teached as a "fun fact" in college or engineering schools), it's really well-known and established. You don't know how to prove that it is bad maths because it's not. You can find flaws in a demonstration of 0.99999.... = 1 but you will always find other ways to prove it, but not the contrary. Example (I did'n't read the whole subject, sorry if already mentioned) : 1/3 = 0.333333333333... 3*(1/3) = 3*0.3333333333.... 3*(1/3) = 1 3*0.3333333333333.... = 0.999999999999... So 0.9999999999... = 1 |
Its just rounding it upwards.
there would be a infinite amount of 9s, but there would always also be a part missing.
The reason we can say 0.999999.... = 1 is because our minds cant comprehend infinity,
and it serves no practical perpose to not just accept 0.999... as 1.
That doesnt mean its true though.
1 is a perfect number, infinite 1.00000...
0.9999... isnt ever perfect, even if the 9s go on forever, and your mind cant comprehend there to be a differnce.
It starts out behinde, so even if it goes forever close to 1, it never is.
| Davman said: Well the limit -> infinity is 1 not just x. it was misleading. |
OP was using "x" as a variable to represent a repeating decimals of 9 ...
I don't blame him since he was using it to show an algebraic proof ... 
Well i don't blame him either just got confused for 1 sec.
In maths 0,99999... isn't equal to 1 thats all.
For me this is more mind boggling. Sum of only positives gives you a negative number... theeee fuck