By using this site, you agree to our Privacy Policy and our Terms of Use. Close

Forums - General - Horizontal Stretches/Compression (Math Question).

miz1q2w3e on 20 February 2013
Jay520 said:
miz1q2w3e said:

It makes sense that the graph's behavior would change when transitioning from positive to negative, as well as the other special threshold in this case which is the number 1 (since we are multiplying). Take a number X, where (inf. > abs(x) > 1), here it means that it is raised to a positive power, and (1 > abs(x) > 0) means a negative power.

Scaling (stretching) depends on the absolute value of the scaling factor, and how it relates to the number one. Flipping depends on whether the factor is positive, or negative. Apply at the same time and you get all those changing intervals, notice the change at each threshold.

(1 - inf.) = compressed, non-flipped.
[1] = equal, non-flipped.
(0 - 1) = stretched , non-flipped.

[0] = no graph i.e. a single point.

(-1 - 0) = stretched , flipped.
[-1] = equal, flipped.
(-inf. - -1) = compressed, flipped.

Also, the same does happen with vertical stretching. However, in the case of shifting, we are not multiplying, so the number 1 is no longer a critical point of concern, only the sign of the factor.

Huh? The same doesn't happen with vertical stretching. The direction of the graph correlates with whether the positivity/negativity of A in Af(x).

In vertical stretching, as A decreases the graph is pulled downward. Even as A goes negative, the graph continues to go downward. The opposite is true when positive of course.

This is different from horizontal stretching. As A in f(Ax) decreases, the graph widens away from the Y-axis (assuming the graph is symetrical along the Y axis), but once it hits zero, it stops widening away from the Y-axis and begins to shrink toward the Y-axis

Another thing; yes it begins to shrink, but it is still technically stretched at the point after it hits zero but before it goes past negative 1. Whether is is expanding or shrinking at that moment depends on which way you are coming from.



Around the Network
Jay520 on 20 February 2013
miz1q2w3e said:

This is impossible since, like Osc89 said, a vertical stretch is just a horizontal compression.

...Define vertical stretching?

@bolded, what you're describing sounds like shifting...


A vertical stretch is only a horizontal compression sometimes. For example, take this graph:

A vertical stretch would look like this: (Stretched by 2)

While a horizontal compression would look like this: (Compressed by 2)

 

As you can see, the vertical stretch and horizontal compression are different.

By vertical stretching, I mean this:

changing f(x) = (x+2)^2 to f(x) = 2(x+2)^2

While by horizontal stretching, I mean this:

changing f(x) = (x+2)^2 to f(x) = (x/2 + 2)^2..

-

I will come back later to better express myself with graphs.



miz1q2w3e on 21 February 2013
Jay520 said:
miz1q2w3e said:

This is impossible since, like Osc89 said, a vertical stretch is just a horizontal compression.

...Define vertical stretching?

@bolded, what you're describing sounds like shifting...


A vertical stretch is only a horizontal compression sometimes. For example, take this graph:

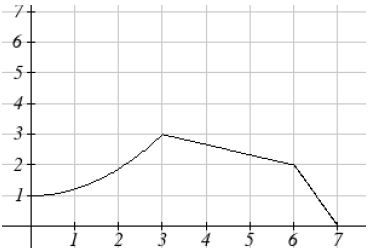
A vertical stretch would look like this: (Stretched by 2)

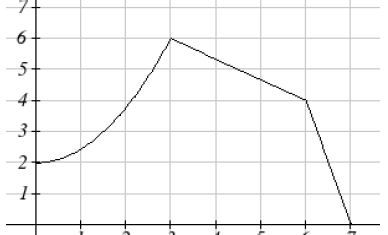
While a horizontal compression would look like this: (Compressed by 2)

 

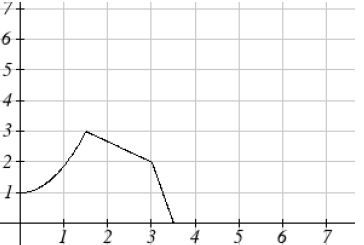
As you can see, the vertical stretch and horizontal compression are different.

By vertical stretching, I mean this:

changing f(x) = (x+2)^2 to f(x) = 2(x+2)^2

While by horizontal stretching, I mean this:

changing f(x) = (x+2)^2 to f(x) = (x/2 + 2)^2..

-

I will come back later to better express myself with graphs.

Look at the last two pics. They are practically the same graph now, albeit on different scales. I think you have issue with calling these two graphs "the same"? They just look, and behave, the same.

Your equations also show the relationship between vertical/horizontal scaling. You see the factor in the first equation has an absolute value greater than 1. You call this vertical stretching, but it is at the same time horizontal compression (see the intervals from my previous post).

In the second equation, the factor has an absolute value less than 1, and it results in horizontal stretching, aka vertical compression. Note that dividing by 2 is the same as multiplying by 0.5

Either way, the phenomenon you mentioned in the op WILL happen with vertical scaling, I have no doubt about this.

If you want to see this, just google you equation, i.e. type your equation into google, and see the results. You will notice that it displays the same (looking) graph for each case, it compresses and stretches based on the coefficient, and it flips when going from positive to negative. Do it in different tabs to compare.

y = 5*x^3, y = 1*x^3, y = 0.5*x^3, y = 0*x^3, y = -0.5*x^3, y = -1*x^3, y = -5*x^3

OR if you really think it makes a differece:

y = (x/0.2)^3, y = (x/1)^3, y = (x/2)^3, y = (x*0)^3, y = (x/-2)^3, y = (x/-1)^3, y = (x/-0.2)^3